「相対論 超概論」

2011年10月01日作成　 　1page　　2page　　3page　

特殊相対性理論の原理

アインシュタインは、1905年の論文「動いている物体の電気力学」において特殊相対性理論を発表しました。論文のタイトルには相対性などという言葉は出てこないのですが、電気力学つまり電磁気学の在り方こそが論点の核心であったことは前述の通りです。

アインシュタインは、この論文において次の2点を原理、つまり理論の前提として提唱しています。

●すべての慣性系で、物理法則は同じ形を取る。

● 真空中の光の速度cは光源の運動に無関係で、一定である。

最初の原理は今日では"特殊相対性原理"と呼ばれます。それまでの物理学では、既に確立した理論に対しある座標変換を施して物理法則が同じ形になるかどうかを議論していましたが、アインシュタインは議論をいわばひっくり返して、物理法則が同じになることを原理として要求したのです。この原理によると、全ての慣性系は互いに同等であり、異なった運動をする慣性系の間で物理現象の解釈が様々であったとしても、それらは「相対的に」正しいということになります。また、座標系の運動状態は無数に考えられますが、今は慣性系、つまり等速直線運動をしている座標系という「特殊な」場合に限定しています。これが、「特殊相対性」という名称の意味するところです。

2番目の原理は"光速度不変の原理"と言います。なぜいきなり光の速度が出てくるのかと思われるかもしれないので説明しますと、マックスウェル電磁気学では光は電場と磁場が交互に変化する波、つまり電磁波として表わされます。そして、波の一般的な性質として、波の速度は波源の運動には無関係です。つまり、光速度不変の原理は、力学と電磁気学の矛盾を解決する上記の2つの方法のうち、光を電磁波とするマックスウェル電磁気学の立場を正しいとする後者の立場を採用していると解することができます。

これらの原理から理論を展開して、アインシュタインは様々な興味深い結果を導出しています。では、その結果の一部を見ていきましょう。

長さの収縮と時間の遅れ

アインシュタインは、特殊相対性原理と光速度不変の原理から出発して、ローレンツ変換を再発見し、その物理的な意味を明確にしました。特殊相対性原理の要請からすると、慣性系の間の座標変換はガリレイ変換ではなくローレンツ変換であり、これに基づいてニュートン力学は修正される必要があります。このようにして導出された理論的帰結の1つに、運動している物体の長さが収縮する、また時間が遅れるという有名な概念があります。もちろんここで言う運動とは等速直線運動のことです。正確に言うと、運動している座標系（以下運動系といいます）と静止した座標系（以下静止系といいます）の間で座標変換を行うとこのような結果になるという意味です。

もう少し詳しく説明しましょう。そのために、まずローレンツ変換の具体的な形を見ることにしましょう。先ほどと同様に、Aから見てBがX軸方向に速度vで運動しているとき、AとBの間のローレンツ変換は、

で与えられます（≡ は左辺を右辺で定義するという意味の記号です）。長さの次元を持つxに合わせるため、時間tに光速度cが掛けられていることに注意してください。速度は長さを時間で割ったものですから、これを時間に掛ければ、残る次元は長さになります。

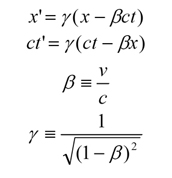
上の式を見れば分かるように、ローレンツ変換の形式はガリレイ変換より少し複雑であり、また時間tは両方の座標系で不変ではなく、空間座標xに依存して変化します。したがって、相対論ではニュートン力学での絶対時間という概念は存在せず、各座標系において時間の進み方は相対的になります。また、βとγの形式から、vはcと等しい値を取ることはできないことも分かります。仮にv = cとすると、γは無限大となってしまうからです。よって、どんな物体も光速度まで加速することはできないということになります。

さて、まず長さが収縮するとは、2点間の距離が短くなるということです。これはxについてのローレンツ変換から導かれます。速度vの運動系でX軸上の座標x'₁と座標x'₂ の間の距離がLであったとしましょう。つまり、

です。これを静止系から見るとどうなるかは、x'₁、x'₂それぞれにローレンツ変換の式を当てはめて静止系の座標x'₁、x'₂を導出し、その間の距離を計算すれば分かります。すると、静止系でのある時刻tにおいて、

となりますから、明らかに、

となります。一般にv ＜ cなので、β＜ 1が成り立つことに注意してください。したがって、静止系から観測した2点間の距離は、運動系での距離よりも短くなり、言い換えると長さが収縮して見えるのです。

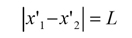
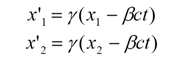
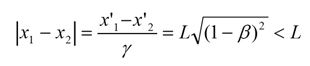
時間の遅れも同様に、時間についてのローレンツ変換から導かれます。上記のローレンツ変換は、Bの座標をAの座標で表わした形になっていますが、これを変形して、Aの座標をBの座標で表わすことにしましょう。簡単な計算により、Aの時間ctについて、

となることが分かります。2つの座標系における経過時間を比較するとしましょう。そのため、A が持っている時計に合わせた時計をあらかじめB の移動先に設置しておき、時間t'後にその時計とBの時計を比較するとします。さて、B自身はBの座標系の原点にいますから、x' = 0です。すると、

が結論されます。ここでのtは、Aが持っている時計に合わせてある時計の読みです。0 ＜ v ＜ cならγ＜ 1なので、t ＜ t'となります。したがって、静止系の時計で計った時間は、運動系の時計で計った時間より長くなり、言い換えると運動系の時間は遅れるということになります。

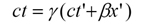
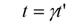
では、なぜ日常的にはこのような現象が体感されないのでしょうか。それは、cが秒速約30万kmというとてつもなく大きな値であるのに対し、私たちが通常関わる速度はそれよりもずっと小さいからです。すると、βはほぼ0、γはほぼ1になり、長さも時間も運動系と静止系の間でほとんど同じということになります。この場合はニュートン力学を適用してほぼ精確に物理現象を記述することができます。つまり、ニュートン力学は相対論でvをcに比べて非常に小さくした場合の近似理論であり、逆にv がc に近くなると相対性理論を適用する必要が生じます。