「相対論 超概論」

2011年10月01日作成　 　1page　　2page　　3page　

鈴木 隆平

今年2011年は、相対性理論にとって記念すべき年に当たります。アルバート・アインシュタインの論文「光の伝播に対する重力の影響」が発表されてから100周年になるからです。この論文以後アインシュタインは数年をかけて一連の論文を発表し、それらの論文によって20世紀物理学の金字塔のひとつである一般相対性理論が確立されたのでした。

とはいえ、相対性理論という名前を聞いたことがある人はかなりいると思われますが、それが何についてのどのような理論なのかを知っている人はあまり多くないのではないでしょうか？例えば、一般相対性理論の「一般」とは何なのでしょう？一般ではない相対性理論があるということでしょうか？そもそも、「相対性」とは何が何に対して相対的と言っているのでしょうか？

相対性理論は自然界の4つの基本的な力のうち、重力を説明する理論です。また、きわめて美しい構造を持っており、物理学の理論とはこうあるべきだ、というお手本のような存在です。相対性理論を本当に理解しようとしたら、やはり専門書を読んで難しい方程式と向き合う必要があるのですが、「相対性理論ってこんな理論だよ」と言葉で説明することも不可能ではないと思います。そこで、今回は相対性理論のエッセンスを、なるべく簡潔にご紹介したいと思います。

物理学の大前提と歴史

そもそも物理学が成立するためには、基本となる大前提が存在します。その大前提とは、「自然界の法則は、方程式を用いて数学的に表現できる」 というものです。自然界の秩序を表現するのに、数学の論理性が有用だということは大昔から知られており、数学の歴史と物理学の歴史を切り離して考えることはできません。もっとも、よくよく考えてみると、人間が生み出した概念に過ぎない数学が、人間の知的活動とは無関係に存在する自然界を記述できるというのは非常に不思議な話なのですが、それはともかく、数学と物理学は相互に刺激しあって発展していき、物理法則を表現するための数学的手段が次々に開発されていきました。古代ギリシャから中世にかけては幾何学、近世以降は微積分学が大いに発展し、自然の法則は関係する物理量をパラメーターとする微分方程式で表現されるという認識が確立しました。物体の運動を記述するとは、この微分方程式を解くことと等価なのです。

こうして19世紀の後半までに、物理学の2つの分野における基礎方程式が確立されました。重力下の物体の運動を記述する力学では、アイザック・ニュートンが定式化した、質量と加速度の積が力に等しいという有名な"ニュートン方程式"、電気と磁気の振る舞いを記述する電磁気学ではジェームズ・クラーク・マックスウェルによる"マックスウェル方程式"が、それぞれの分野の基礎方程式となりました。これらの方程式とその応用から、当時知られていた物理現象はすべて説明できるように見えたので、一時は物理学はこれで完成した、あるいは完成間近だという人もいたようです。これが相対性理論前夜の状況でした。

力学と電磁気学の矛盾

とはいえ、これで安心できなかった人もいました。力学と電磁気学は、対象とする物理現象が異なっており、同じ宇宙の違った側面を記述しているわけですが、この2つの理論の間に矛盾がないと言えるのでしょうか？同じ宇宙の物理法則を説明する理論なのに、理論の間に矛盾があったとしたら、少なくともどちらかの理論は修正を必要とするのではないでしょうか。

実際、19世紀の終わりまでには、ニュートン方程式とマックスウェル方程式の間に矛盾があることが知られていました。その矛盾とは、ある観測者が自分を中心とした座標系で観測した物理現象を、他の観測者が観測するとどうなるか、という問題に関連しています。

同じ物理現象を観測していても、観測者によって現象の解釈が異なる、というのは珍しいことではありません。例えば、静止している人Aの前を車が通り過ぎたとしましょう。Aから見ると、自分は止まっているのに対し車は動いている、ということになりますが、車に乗っている人Bから見ると、Bと車は静止していて、Aを含めた回りの景色が動いているのだ、と主張することも可能です。自分を中心とした現象の説明としては、AもBも首尾一貫しており、相対的に正しいと言えます。

この相対性を物理理論で表現したらどうなるでしょうか。AとBの立場の違いは数学的には座標系の違いとして表現されるでしょう。この座標系の間でパラメーターの変換則を設定することにより、座標系AとBの立場を相互に「翻訳」することが可能になります。この変換則を理論の方程式のパラメーターに適用すれば、方程式自体の「翻訳」を行ったことになります。翻訳の結果、Aの座標系での方程式と、Bの座標系での方程式の形に変化がなければ、AとBに対して同じ方程式、同じ理論を適用できることになります。

一口に座標系の違いといっても、実際には無数のパターンがあるわけですが、一番簡単なのはAから見てBが等速直線運動、つまり加速度の無い運動をしている場合です。もちろん、Bから見た場合はAが等速直線運動をしているということになります。AまたはBの運動は、各自を原点とした座標系の運動として表現することができます。以後、この等速直線運動をする座標系の事を"慣性系"と呼びます（ニュートンの慣性の法則が成り立つ座標系という意味です）。

力学と電磁気学の矛盾とは、この慣性系における座標変換に関わる問題でした。この矛盾を解決する過程で、相対性理論が誕生したのです。では、その矛盾について解説していくことにしましょう。

ガリレイ変換とそれに対する不変性

ある時刻でAとBがX軸上の同じ位置xにおり、Aは静止したままですが、Bは一定の速度vでX軸の方向へ移動していくとします。時間tが経過した後のBの位置は、Aから見るとどのように表わされるでしょうか？単純に考えると、距離が時間と速度の積で表わされるという関係から、Bは位置xからvtだけ進んでいるでしょう。したがって、Bの座標に' を付けて表わすことにすると、AとBの座標の間の関係は、

と表現されます。即ちこれが、AとBの間の最も単純な変換則であり、"ガリレイ変換"と呼ばれます。今の例ではAは静止しているとしましたが、必ずしも静止している必要はなく、AもX軸上を等速直線運動しているとしても構いません。その場合、上記の式のvをAとBの相対速度に置き換えれば、ガリレイ変換はそのまま適用できます。つまり、ガリレイ変換は任意の慣性系の間の変換則と考えられます。ここでは説明しませんが、この変換則をニュートン方程式に適用したとき、変換後の方程式の形が不変であることを確かめることができます。

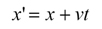
注意したい点が2つあります。1つ目は、今の論理において時間tは2つの慣性系で共通と仮定していることです。Aの手元にある時計と、Bの手元にある時計は同じ時を刻んでおり、お互いに自分の時計を見ることで相手の時間を知ることができるという仮定です。式で表わすと、

ということになります。ニュートン力学ではこの共通の時間の流れは全宇宙で一様であるとしており、"絶対時間"と呼んでいます。2つ目に注意したいのは、今までの議論は私達の日常の感覚をニュートン力学に当てはめた結果であるということです。ニュートン力学の理論の前提としてガリレイ変換不変性が要求されているわけではなく、私たちが感覚的に成り立っていると期待する関係をニュートン方程式に適用したら、結果として不変であったにすぎないというわけです。

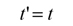
こうしてニュートン方程式にガリレイ変換不変性があることを確認できたので、マックスウェル方程式にも同様の結果が成り立つと期待したくなります。しかし、困ったことに、マックスウェル方程式にガリレイ変換を適用した結果は、方程式の形が全く変わってしまうのです。これこそが2つの方程式の間の、ひいては力学と電磁気学の矛盾でした。 力学と電磁気学が両方間違っているという可能性もありますが、仮にどちらか一方は正しいとすると、この矛盾を解決するには次の2通りの解決策が考えられます。

　1．ニュートン力学が正しく、マックスウェル電磁気学はガリレイ変換に対して不変になるように修正されるべき。

　2．マックスウェル電磁気学が正しい。ガリレイ変換とは別の、マックスウェル方程式を不変にするような変換が存在し、ニュートン力学はその変換に対して不変になるように修正されるべき。

2番目の可能性にある、マックスウェル方程式を不変にする変換は実際に提唱され、今日では提唱者の名前を取って"ローレンツ変換"と呼ばれています。しかし、そのような変換を正当化する根拠はありませんでした。もっとも、ガリレイ変換自体を正当化する根拠も特に無かったのですが、ガリレイ変換は私達の感覚に合致しているので、ガリレイ変換に修正を強いるにはそれなりの根拠が求められたのです。まさにその根拠を提示し、論理的に明快な方法で矛盾を解消したのがアインシュタインの特殊相対性理論でした。